关于海纳ABOUT HAINER
MORE+海纳教育成立于 2007 年,学校坐落在历史文化名城、商贸物流之都、滨水生态之城、红色旅游城市——山东临沂。
现培训项目主要包括:高考志愿填报、专升本辅导、考研辅导、计算机等级培训等。现拥有占地20000平米的教学大楼,现代化多媒体教室、5000平米的校园智能餐厅,5000平米的室内健身训练馆、豪华宿舍,宿舍配备中央空调、独立卫生间。全套教学硬件设施一应俱全。
高考填报ADMISSIONS GUIDE
MORE+
各位考生:你们好!山东省2019年普通高等教育专科升本科招生考试在即,为保证你们能够顺利完成考试,特提醒如下:一、牢记考

信息公告ANNOUNCEMENT
MORE+山东省2020年专升本专业类别设置及考试科目招生专业所属学科门类代码招生专业所属学科门类(考试门类)考试科目01哲学1.
报考指南APPLY FOR
MORE+
校园动态DYNAMIC
MORE+让我们回忆去年我们在一起的点点滴滴,用文字记录升本路上的成长故事,尽情畅谈自己的升本之路
学员寄语MESSAGE
MORE+既然要还自己一个本科梦,可千万要有始有终
我们总喜欢拿顺其自然来敷衍人生道路上的荆棘坎坷,却很少承认,真正的顺其自然,其实是竭尽所能后的不强求
法规政策REGULATION
MORE+
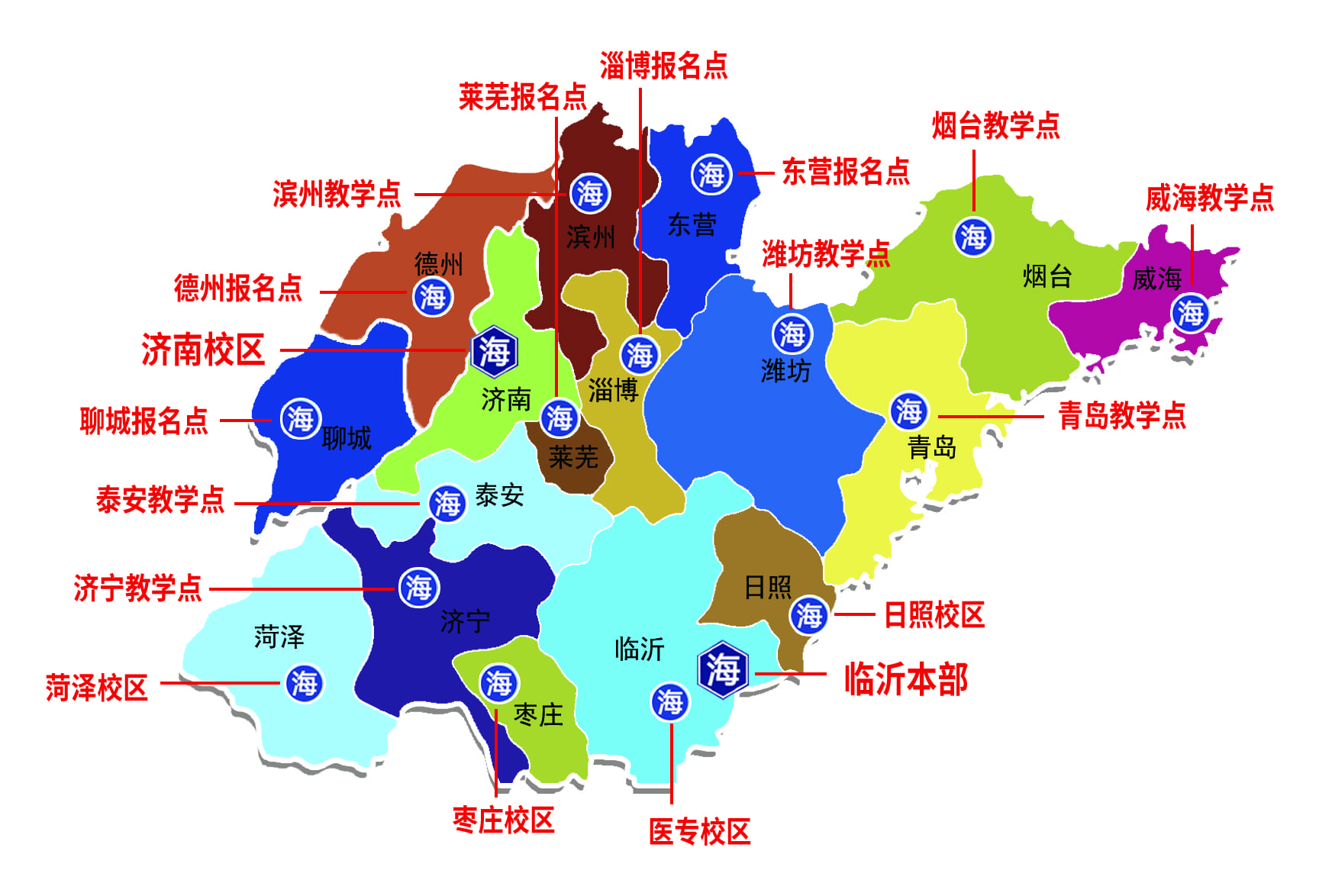
Copyright ©2024 海纳教育 ALL rights Reserved. 备案号:鲁ICP备20012951号-1 图片来源于网络,如有侵权,请及时联系删除! 技术支持:智顺网络
